Example
Neighborhood collective communication in a Cartesian virtual topology.
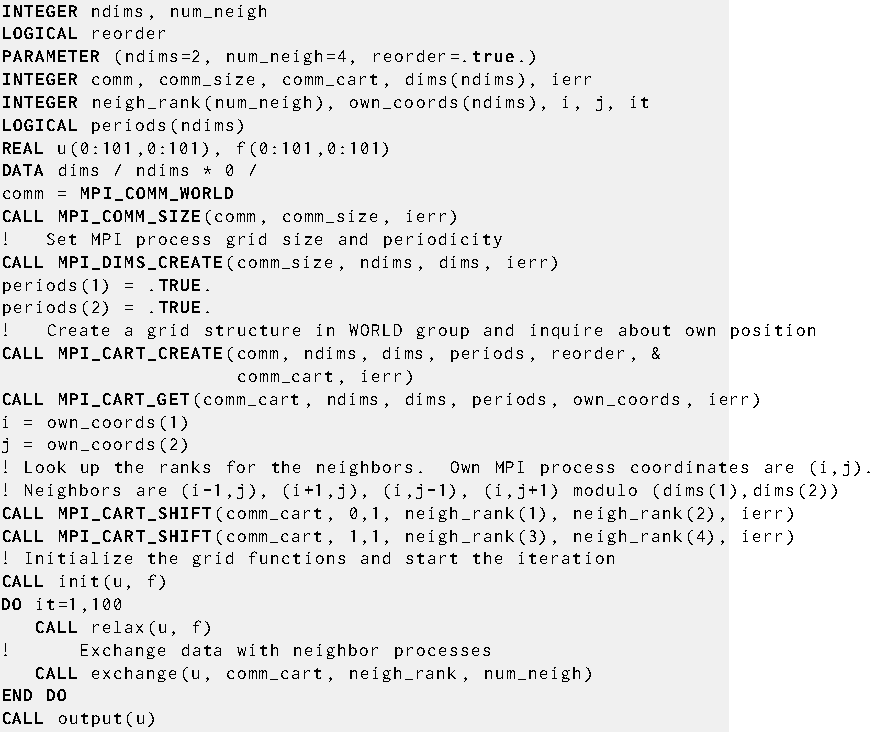
The example in Figures An Application Example--An Application Example shows how the grid definition and inquiry functions can be used in an application program. A partial differential equation, for instance the Poisson equation, is to be solved on a rectangular domain. First, the MPI processes organize themselves in a two-dimensional structure. Each MPI process then inquires about the ranks of its neighbors in the four directions (up, down, right, left). The numerical problem is solved by an iterative method, the details of which are hidden in the subroutine relax.
In each relaxation step each MPI process computes new values for the solution grid function at the points u(1:100,1:100) owned by the MPI process. Then the values at inter-process boundaries have to be exchanged with neighboring MPI processes. For example, the newly calculated values in u(1,1:100) must be sent into the halo cells u(101,1:100) of the left-hand neighbor with coordinates (own_coord(1)-1,own_coord(2)).

Set-up of MPI process structure for two-dimensional
parallel Poisson solver
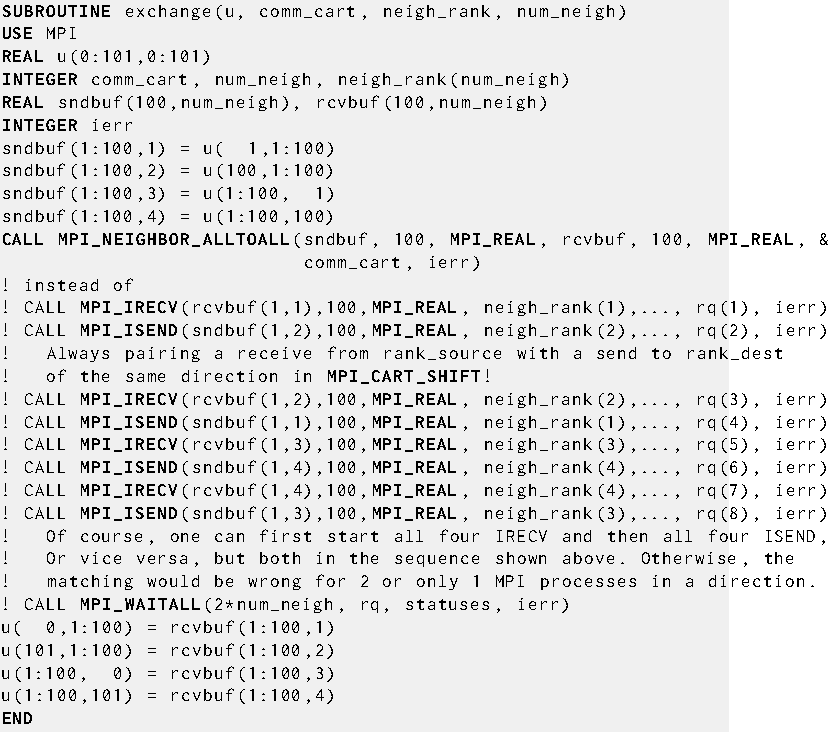
Communication routine with local data copying and sparse neighborhood alltoall
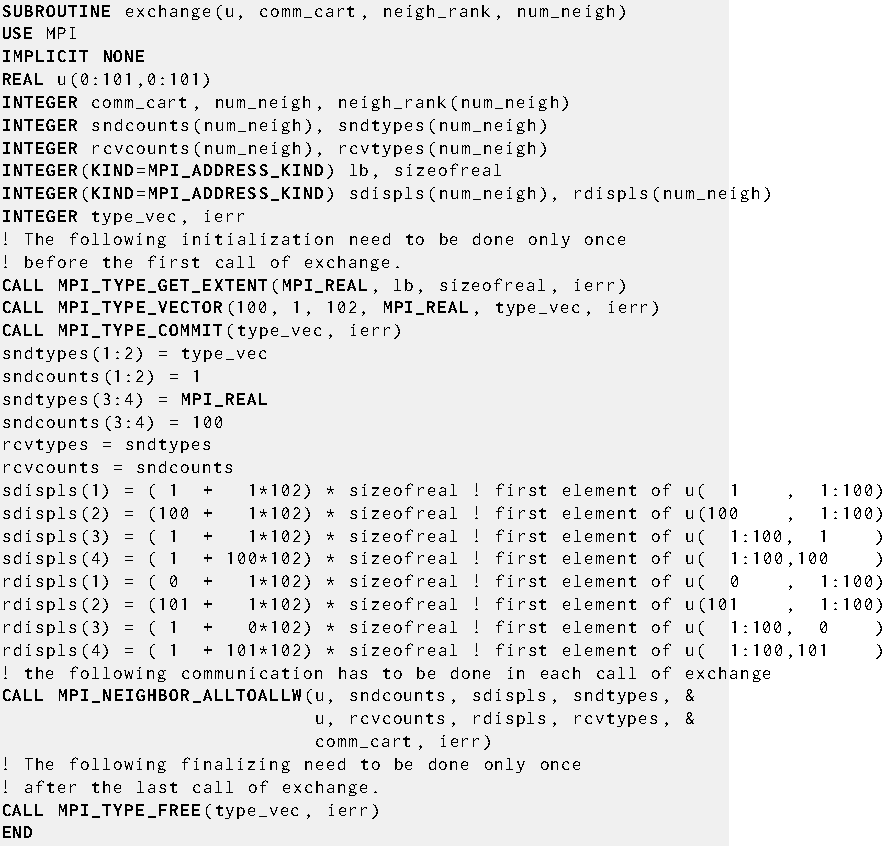
Communication routine with sparse neighborhood alltoallw and without local data copying
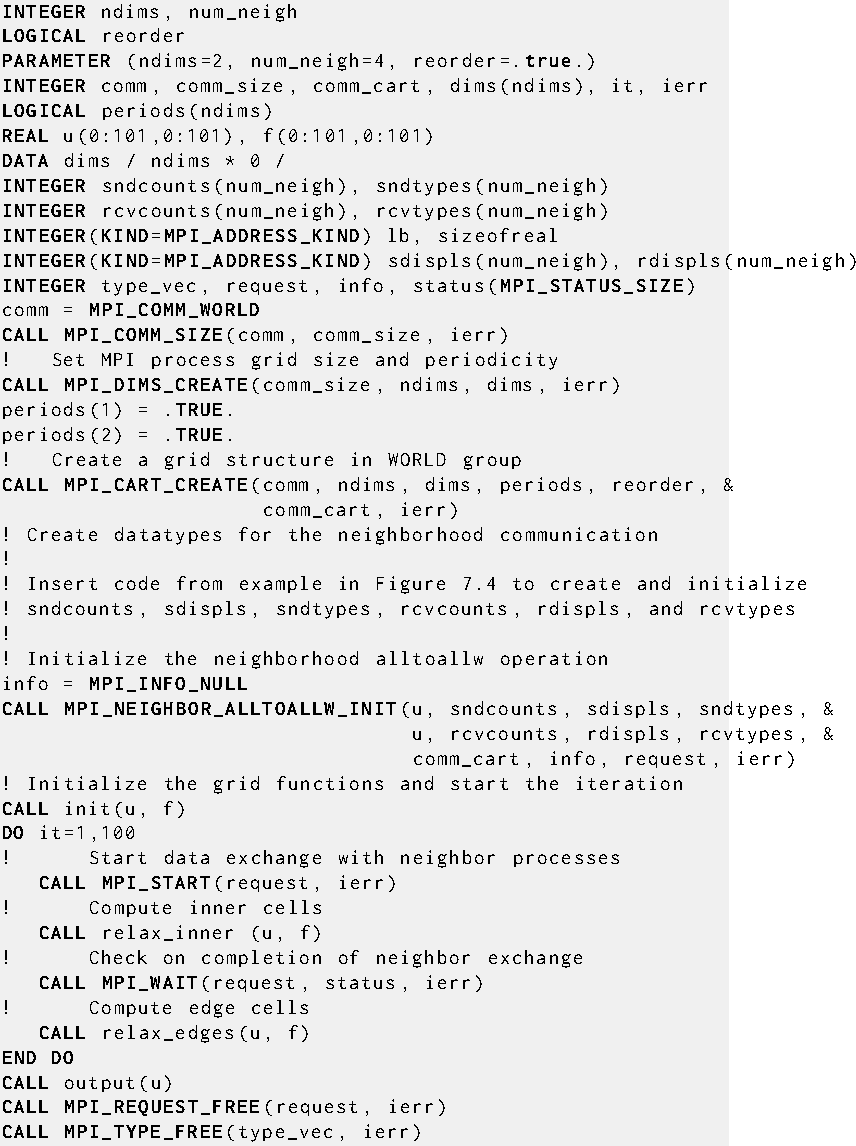
Two-dimensional parallel Poisson solver with persistent sparse neighborhood alltoallw and without local data copying