194. An Application Example

Example The example in Figures 18 -An Application Example shows how the grid definition and inquiry functions can be used in an application program. A partial differential equation, for instance the Poisson equation, is to be solved on a rectangular domain. First, the processes organize themselves in a two-dimensional structure. Each process then inquires about the ranks of its neighbors in the four directions (up, down, right, left). The numerical problem is solved by an iterative method, the details of which are hidden in the subroutine relax.

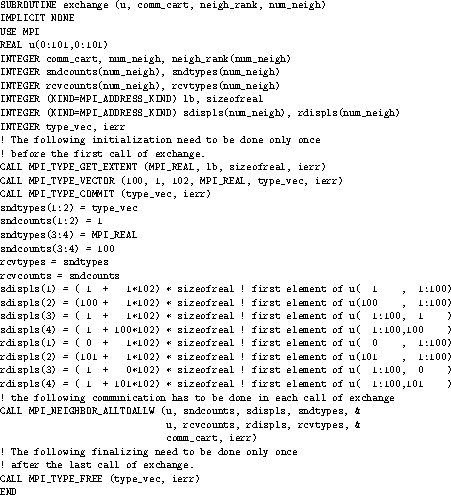
In each relaxation step each process computes new values for the solution grid function at the points u(1:100,1:100) owned by the process. Then the values at inter-process boundaries have to be exchanged with neighboring processes. For example, the newly calculated values in u(1,1:100) must be sent into the halo cells u(101,1:100) of the left-hand neighbor with coordinates (own_coord(1)-1,own_coord(2)).

INTEGER ndims, num_neigh 
LOGICAL reorder 
PARAMETER (ndims=2, num_neigh=4, reorder=.true.) 
INTEGER comm, comm_cart, dims(ndims), ierr 
INTEGER neigh_rank(num_neigh), own_coords(ndims), i, j, it 
LOGICAL periods(ndims) 
REAL u(0:101,0:101), f(0:101,0:101) 
DATA dims / ndims * 0 / 
comm = MPI_COMM_WORLD 
!   Set process grid size and periodicity 
CALL MPI_DIMS_CREATE(comm, ndims, dims, ierr) 
periods(1) = .TRUE. 
periods(2) = .TRUE. 
!   Create a grid structure in WORLD group and inquire about own position 
CALL MPI_CART_CREATE (comm, ndims, dims, periods, reorder, & 
                      comm_cart, ierr) 
CALL MPI_CART_GET (comm_cart, ndims, dims, periods, own_coords, ierr) 
i = own_coords(1) 
j = own_coords(2) 
! Look up the ranks for the neighbors.  Own process coordinates are (i,j). 
! Neighbors are (i-1,j), (i+1,j), (i,j-1), (i,j+1) modulo (dims(1),dims(2)) 
CALL MPI_CART_SHIFT (comm_cart, 0,1,  neigh_rank(1),neigh_rank(2), ierr) 
CALL MPI_CART_SHIFT (comm_cart, 1,1,  neigh_rank(3),neigh_rank(4), ierr) 
! Initialize the grid functions and start the iteration 
CALL init (u, f) 
DO it=1,100 
   CALL relax (u, f) 
!      Exchange data with neighbor processes 
   CALL exchange (u, comm_cart, neigh_rank, num_neigh) 
END DO 
CALL output (u) 

SUBROUTINE exchange (u, comm_cart, neigh_rank, num_neigh) 
REAL u(0:101,0:101) 
INTEGER comm_cart, num_neigh, neigh_rank(num_neigh) 
REAL sndbuf(100,num_neigh), rcvbuf(100,num_neigh) 
INTEGER ierr  
sndbuf(1:100,1) = u(  1,1:100) 
sndbuf(1:100,2) = u(100,1:100) 
sndbuf(1:100,3) = u(1:100,  1) 
sndbuf(1:100,4) = u(1:100,100) 
CALL MPI_NEIGHBOR_ALLTOALL (sndbuf, 100, MPI_REAL, rcvbuf, 100, MPI_REAL, & 
                            comm_cart, ierr)  
! instead of  
! DO i=1,num_neigh 
!   CALL MPI_IRECV(rcvbuf(1,i),100,MPI_REAL,neigh_rank(i),...,rq(2*i-1),& 
!                  ierr) 
!   CALL MPI_ISEND(sndbuf(1,i),100,MPI_REAL,neigh_rank(i),...,rq(2*i  ),& 
!                  ierr) 
! END DO  
! CALL MPI_WAITALL (2*num_neigh, rq, statuses, ierr) 
  
u(  0,1:100) = rcvbuf(1:100,1)  
u(101,1:100) = rcvbuf(1:100,2)  
u(1:100,  0) = rcvbuf(1:100,3)  
u(1:100,101) = rcvbuf(1:100,4)  
END 

Communication routine with sparse neighborhood all-to-all-w and without local data copying.