MPI_GRAPH_CREATE requires that each MPI process passes the full (global) communication graph to the call. This limits the scalability of this constructor. With the distributed graph interface, the communication graph is specified in a fully distributed fashion. Each MPI process specifies only the part of the communication graph of which it is aware. Typically, this could be the set of MPI processes from which the MPI process will eventually receive or get data, or the set of MPI processes to which the MPI process will send or put data, or some combination of such edges. Two different interfaces can be used to create a distributed graph topology. MPI_DIST_GRAPH_CREATE_ADJACENT creates a distributed graph communicator with each MPI process specifying each of its incoming and outgoing (adjacent) edges in the logical communication graph and thus requires minimal communication during creation. MPI_DIST_GRAPH_CREATE provides full flexibility such that any MPI process can indicate that communication will occur between any pair of MPI processes in the graph.
To provide better possibilities for optimization by the MPI library, the distributed graph constructors permit weighted communication edges and take an info argument that can further influence process reordering or other optimizations performed by the MPI library. For example, hints can be provided on how edge weights are to be interpreted, the quality of the reordering, and/or the time permitted for the MPI library to process the graph.
| MPI_DIST_GRAPH_CREATE_ADJACENT(comm_old, indegree, sources, sourceweights, outdegree, destinations, destweights, info, reorder, comm_dist_graph) | |
| IN comm_old | input communicator (handle) |
| IN indegree | size of sources and sourceweights arrays (non-negative integer) |
| IN sources | ranks of MPI processes for which the calling process is a destination (array of non-negative integers) |
| IN sourceweights | weights of the edges into the calling MPI process (array of non-negative integers) |
| IN outdegree | size of destinations and destweights arrays (non-negative integer) |
| IN destinations | ranks of MPI processes for which the calling MPI process is a source (array of non-negative integers) |
| IN destweights | weights of the edges out of the calling MPI process (array of non-negative integers) |
| IN info | hints on optimization and interpretation of weights (handle) |
| IN reorder | ranks may be reordered ( true) or not ( false) (logical) |
| OUT comm_dist_graph | new communicator with associated distributed graph topology (handle) |
MPI_DIST_GRAPH_CREATE_ADJACENT returns a handle to a new communicator to which the distributed graph topology information is attached. Each MPI process passes all information about its incoming and outgoing edges in the virtual distributed graph topology. The calling MPI processes must ensure that each edge of the graph is described in the source and in the destination process with the same weights. If there are multiple edges for a given ( source, dest) pair, then the sequence of the weights of these edges does not matter. The complete communication topology is the combination of all edges shown in the sources arrays of all MPI processes in comm_old, which must be identical to the combination of all edges shown in the destinations arrays. Source and destination MPI processes must be specified by their rank in the group of comm_old. This allows a fully distributed specification of the communication graph. Isolated MPI processes (i.e., MPI processes with no outgoing or incoming edges, that is, MPI processes that have specified indegree and outdegree as zero and thus do not occur as source or destination in the graph specification) are allowed.
The call creates a new communicator comm_dist_graph of distributed graph topology type to which topology information has been attached. The number of MPI processes in comm_dist_graph is identical to the number of MPI processes in comm_old. The call to MPI_DIST_GRAPH_CREATE_ADJACENT is collective.
Weights are specified as nonnegative integers and can be used to
influence the process mapping strategy and other internal MPI
optimizations. For instance, approximate count arguments of later
communication calls along specific edges could be used as their edge
weights. Multiplicity of edges can likewise indicate more intense
communication between pairs of MPI processes. However, the exact meaning
of edge weights is not specified by the MPI standard and is left to
the implementation. In C or Fortran, an application can supply the
special value MPI_UNWEIGHTED for the weight array to indicate
that all edges have the same (effectively no) weight. It is erroneous to supply
MPI_UNWEIGHTED for some but not all MPI processes of
comm_old.
If the graph is weighted but
indegree or outdegree is zero, then MPI_WEIGHTS_EMPTY or any
arbitrary array may be passed to sourceweights or
destweights respectively. Note that MPI_UNWEIGHTED and
MPI_WEIGHTS_EMPTY are not special weight values; rather they
are special values for the total array argument. In Fortran,
MPI_UNWEIGHTED and MPI_WEIGHTS_EMPTY are objects like
MPI_BOTTOM (not usable for initialization or assignment).
See Section Named Constants.
Advice to users.
In the case of an empty weights array argument passed while constructing
a weighted graph, one should not pass NULL because the value of
MPI_UNWEIGHTED may be equal to NULL. The value of this argument
would then be indistinguishable from MPI_UNWEIGHTED to the
implementation. In this case MPI_WEIGHTS_EMPTY should be used
instead.
( End of advice to users.)
Advice
to implementors.
It is recommended that MPI_UNWEIGHTED not be implemented as
NULL.
( End of advice to implementors.)
Rationale.
To ensure backward compatibility, MPI_UNWEIGHTED may still be
implemented as NULL. See subsec:22to30.
( End of rationale.)
The meaning of the info and reorder arguments is defined
in the description of the following routine.
| MPI_DIST_GRAPH_CREATE(comm_old, n, sources, degrees, destinations, weights, info, reorder, comm_dist_graph) | |
| IN comm_old | input communicator (handle) |
| IN n | number of source nodes for which this MPI process specifies edges (non-negative integer) |
| IN sources | array containing the n source nodes for which this MPI process specifies edges (array of non-negative integers) |
| IN degrees | array specifying the number of destinations for each source node in the source node array (array of non-negative integers) |
| IN destinations | destination nodes for the source nodes in the source node array (array of non-negative integers) |
| IN weights | weights for source to destination edges (array of non-negative integers) |
| IN info | hints on optimization and interpretation of weights (handle) |
| IN reorder | ranks may be reordered ( true) or not ( false) (logical) |
| OUT comm_dist_graph | new communicator with associated distributed graph topology (handle) |
MPI_DIST_GRAPH_CREATE returns a handle to a new communicator to which the distributed graph topology information is attached. Concretely, each MPI process calls the constructor with a set of directed ( source, destination) communication edges as described below. Every MPI process passes an array of n source nodes in the sources array. For each source node, a nonnegative number of destination nodes is specified in the degrees array. The destination nodes are stored in the corresponding consecutive segment of the destinations array. More precisely, if the i-th node in sources is s, this specifies degrees[i] edges (s,d) with d of the j-th such edge stored in destinations[degrees[0]+...+degrees[i-1]+j]. The weight of this edge is stored in weights[degrees[0]+...+degrees[i-1]+j]. Both the sources and the destinations arrays may contain the same node more than once, and the order in which nodes are listed as destinations or sources is not significant. Similarly, different processes may specify edges with the same source and destination nodes. Source and destination nodes must be specified by their rank in the group of comm_old. Different MPI processes may specify different numbers of source and destination nodes, as well as different source to destination edges. This allows a fully distributed specification of the communication graph. Isolated MPI processes (i.e., MPI processes with no outgoing or incoming edges, that is, MPI processes that do not occur as source or destination node in the graph specification) are allowed.
The call creates a new communicator comm_dist_graph of distributed graph topology type to which topology information has been attached. The number of MPI processes in comm_dist_graph is identical to the number of MPI processes in comm_old. The call to MPI_DIST_GRAPH_CREATE is collective.
If reorder = false, all MPI processes will have the same rank in comm_dist_graph as in comm_old. If reorder = true then the MPI library is free to remap to other MPI processes (of comm_old) in order to improve communication on the edges of the communication graph. The weight associated with each edge is a hint to the MPI library about the amount or intensity of communication on that edge, and may be used to compute a ``best'' reordering.
Weights are specified as nonnegative integers and can be used to
influence the MPI process remapping strategy and other internal MPI
optimizations. For instance, approximate count arguments of later
communication calls along specific edges could be used as their edge
weights. Multiplicity of edges can likewise indicate more intense
communication between pairs of MPI processes. However, the exact meaning
of edge weights and multiplicity of edges is not specified by the MPI standard and is left to
the implementation. In C or Fortran, an application can supply the
special value MPI_UNWEIGHTED for the weight array to indicate
that all edges have the same (effectively no) weight. It is erroneous to supply MPI_UNWEIGHTED for some but not all MPI processes of
comm_old.
If the graph is weighted but n = 0, then
MPI_WEIGHTS_EMPTY or any arbitrary array may be passed to
weights. Note that MPI_UNWEIGHTED and
MPI_WEIGHTS_EMPTY are not special weight values; rather
they are special values for the total array argument. In Fortran,
MPI_UNWEIGHTED and MPI_WEIGHTS_EMPTY are objects like
MPI_BOTTOM (not usable for initialization or assignment).
See Section Named Constants.
Advice to users.
In the case of an empty weights array argument passed while constructing
a weighted graph, one should not pass NULL because the value of
MPI_UNWEIGHTED may be equal to NULL. The value of this argument
would then be indistinguishable from MPI_UNWEIGHTED to the
implementation. MPI_WEIGHTS_EMPTY should be used
instead.
( End of advice to users.)
Advice
to implementors.
It is recommended that MPI_UNWEIGHTED not be implemented as
NULL.
( End of advice to implementors.)
Rationale.
To ensure backward compatibility, MPI_UNWEIGHTED may still be
implemented as NULL. See subsec:22to30.
( End of rationale.)
The meaning of the weights argument can be influenced by the
info argument. The info argument can be used to guide the
mapping of MPI processes to the hardware; possible options include minimizing the maximum number of
edges between processes on different SMP nodes, or minimizing the sum
of all such edges. As described in Section The Info Object,
an MPI implementation is not obliged to follow
specific hints, and it is valid for an MPI implementation not to do
any reordering. An MPI implementation may specify more info
( key, value) pairs. All MPI processes must specify the same set of ( key, value)
info pairs.
Advice
to implementors.
MPI implementations must document any additionally supported ( key, value) info pairs. MPI_INFO_NULL is always valid, and may indicate the default creation of the distributed graph topology to the MPI library.
An implementation does not explicitly need to construct the topology
from its distributed parts. However, all MPI processes can construct the
full topology from the distributed specification and use this in a
call to MPI_GRAPH_CREATE to create the topology. This may serve
as a reference implementation of the functionality, and may be
acceptable for small communicators. However, a scalable high-quality
implementation would save the topology graph in a distributed way.
( End of advice to implementors.)
Example
Several ways to specify the adjacency matrix for MPI_DIST_GRAPH_CREATE and MPI_DIST_GRAPH_CREATE_ADJACENT.
As for Example Graph Constructor, assume there are four MPI processes with ranks 0, 1, 2, 3 in the input communicator with the following adjacency matrix and unit edge weights:
| MPI process | neighbors |
| 0 | 1, 3 |
| 1 | 0 |
| 2 | 3 |
| 3 | 0, 2 |
| MPI process | n | sources | degrees | destinations | weights |
| 0 | 1 | 0 | 2 | 1,3 | 1,1 |
| 1 | 1 | 1 | 1 | 0 | 1 |
| 2 | 1 | 2 | 1 | 3 | 1 |
| 3 | 1 | 3 | 2 | 0,2 | 1,1 |
Another way would be to pass the whole graph on MPI process with rank 0 in the input communicator, which could be done with the following arguments per MPI process:
| MPI process | n | sources | degrees | destinations | weights |
| 0 | 4 | 0,1,2,3 | 2,1,1,2 | 1,3,0,3,0,2 | 1,1,1,1,1,1 |
| 1 | 0 | - | - | - | - |
| 2 | 0 | - | - | - | - |
| 3 | 0 | - | - | - | |
In both cases above, the application could supply MPI_UNWEIGHTED instead of explicitly providing identical weights.
MPI_DIST_GRAPH_CREATE_ADJACENT could be used to specify this graph using the following arguments:
| MPI process | indegree | sources | sourceweights | outdegree | destinations | destweights |
| 0 | 2 | 1,3 | 1,1 | 2 | 1,3 | 1,1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 2 | 1 | 3 | 1 | 1 | 3 | 1 |
| 3 | 2 | 0,2 | 1,1 | 2 | 0,2 | 1,1 |
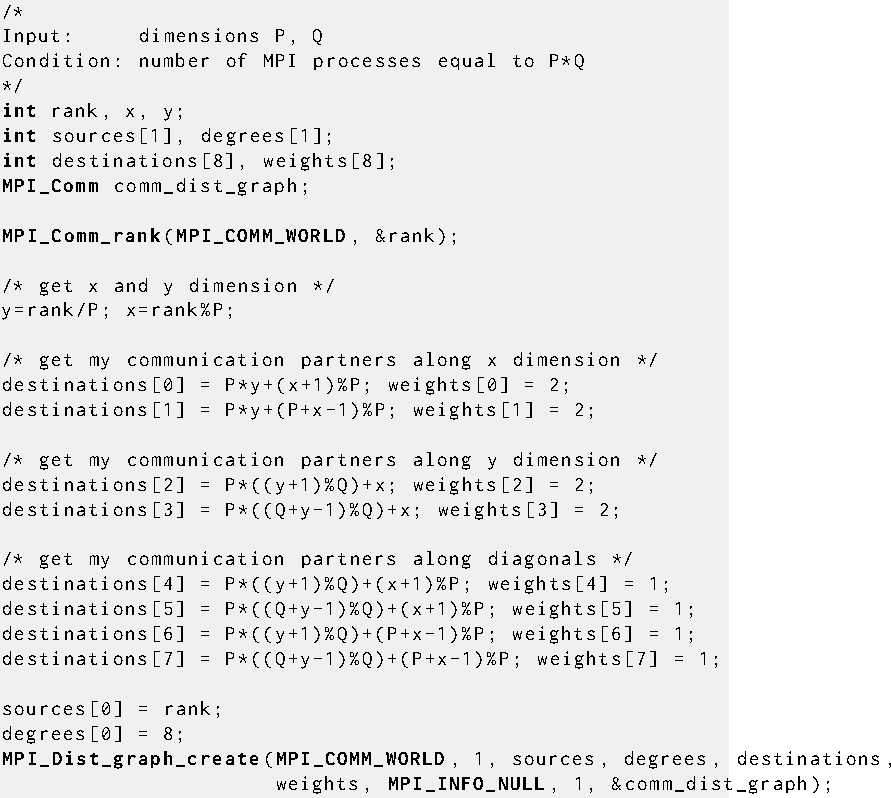
Example
Cartesian grid plus diagonals specified with MPI_DIST_GRAPH_CREATE.
A two-dimensional P × Q torus where all MPI processes communicate along the dimensions and along the diagonal edges cannot be modeled with Cartesian topologies, but can easily be captured with MPI_DIST_GRAPH_CREATE as shown in the following code. In this example, the communication along the dimensions is twice as heavy as the communication along the diagonals:
