MPI provides two approaches to constructing groups. In the first approach, MPI procedures are provided to subset and superset existing groups. These constructors construct new groups from existing groups. In the second approach, a group is created using a session handle and associated process set. This second approach is available when using the Sessions Model. With both approaches, these are local operations, and distinct groups may be defined on different MPI processes; an MPI process may also define a group that does not include itself. Consistent definitions are required when groups are used as arguments in communicator creation functions. When using the World Model (Section The World Model) for MPI initialization, the base group, upon which all other groups are defined, is the group associated with the initial communicator MPI_COMM_WORLD (accessible through the function MPI_COMM_GROUP).
Rationale.
In what follows, there is no group duplication function analogous to
MPI_COMM_DUP, defined later in this chapter. There is no need for
a group duplicator. A group, once created, can have several references to it
by making copies of the handle. The following constructors address the need
for subsets and supersets of existing groups.
( End of rationale.)
Advice
to implementors.
Each group constructor behaves as if it returned a new group object.
When this new group is a copy of an existing group, then
one can avoid creating such new objects, using
a reference-count mechanism.
( End of advice to implementors.)
| MPI_COMM_GROUP(comm, group) | |
| IN comm | communicator (handle) |
| OUT group | group corresponding to comm (handle) |
MPI_COMM_GROUP returns in group a handle to the group of comm.
| MPI_GROUP_UNION(group1, group2, newgroup) | |
| IN group1 | first group (handle) |
| IN group2 | second group (handle) |
| OUT newgroup | union group (handle) |
| MPI_GROUP_INTERSECTION(group1, group2, newgroup) | |
| IN group1 | first group (handle) |
| IN group2 | second group (handle) |
| OUT newgroup | intersection group (handle) |
| MPI_GROUP_DIFFERENCE(group1, group2, newgroup) | |
| IN group1 | first group (handle) |
| IN group2 | second group (handle) |
| OUT newgroup | difference group (handle) |
The set-like operations are defined as follows:
| MPI_GROUP_INCL(group, n, ranks, newgroup) | |
| IN group | group (handle) |
| IN n | number of elements in array ranks (and size of newgroup) (integer) |
| IN ranks | ranks of processes in group to appear in newgroup (array of integers) |
| OUT newgroup | new group derived from above, in the order defined by ranks (handle) |
The function MPI_GROUP_INCL creates a group newgroup that consists of the n MPI processes in group with ranks ranks[0],..., ranks[n-1]; the MPI process with rank i in newgroup is the MPI process with rank ranks[i] in group. Each of the n elements of ranks must be a valid rank in group and all elements must be distinct, or else the program is erroneous. If n~=~0, then newgroup is MPI_GROUP_EMPTY. This function can, for instance, be used to reorder the elements of a group. See also MPI_GROUP_COMPARE.
| MPI_GROUP_EXCL(group, n, ranks, newgroup) | |
| IN group | group (handle) |
| IN n | number of elements in array ranks (integer) |
| IN ranks | array of integer ranks of MPI processes in group not to appear in newgroup |
| OUT newgroup | new group derived from above, preserving the order defined by group (handle) |
The function MPI_GROUP_EXCL creates a group of MPI processes newgroup that is obtained by deleting from group those MPI processes with ranks ranks[0],..., ranks[n-1]. The ordering of MPI processes in newgroup is identical to the ordering in group. Each of the n elements of ranks must be a valid rank in group and all elements must be distinct; otherwise, the program is erroneous. If n~=~0, then newgroup is identical to group.
| MPI_GROUP_RANGE_INCL(group, n, ranges, newgroup) | |
| IN group | group (handle) |
| IN n | number of triplets in array ranges (integer) |
| IN ranges | a one-dimensional array of integer triplets, of the form (first rank, last rank, stride) indicating ranks in group of MPI processes to be included in newgroup |
| OUT newgroup | new group derived from above, in the order defined by ranges (handle) |
If ranges consists of the triplets
(first1 , last1, stride1) , ... , (firstn, lastn, striden)
then newgroup consists of the sequence of MPI processes in group with ranks
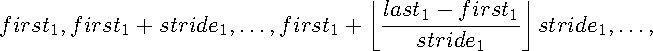

Each computed rank must be a valid rank in group and all computed ranks must be distinct, or else the program is erroneous. Note that we may have firsti > lasti, and stridei may be negative, but cannot be zero.
The functionality of this routine is specified to be equivalent to expanding the array of ranges to an array of the included ranks and passing the resulting array of ranks and other arguments to MPI_GROUP_INCL. A call to MPI_GROUP_INCL is equivalent to a call to MPI_GROUP_RANGE_INCL with each rank i in ranks replaced by the triplet (i,i,1) in the argument ranges.
| MPI_GROUP_RANGE_EXCL(group, n, ranges, newgroup) | |
| IN group | group (handle) |
| IN n | number of triplets in array ranges (integer) |
| IN ranges | a one-dimensional array of integer triplets, of the form (first rank, last rank, stride) indicating ranks in group of MPI processes to be excluded from the output group newgroup (array of integers) |
| OUT newgroup | new group derived from above, preserving the order in group (handle) |
Each computed rank must be a valid rank in group and all computed ranks must be distinct, or else the program is erroneous.
The functionality of this routine is specified to be equivalent to expanding the array of ranges to an array of the excluded ranks and passing the resulting array of ranks and other arguments to MPI_GROUP_EXCL. A call to MPI_GROUP_EXCL is equivalent to a call to MPI_GROUP_RANGE_EXCL with each rank i in ranks replaced by the triplet (i,i,1) in the argument ranges.
Advice to users.
The range operations do not explicitly enumerate ranks, and therefore
are more scalable if implemented efficiently. Hence, we recommend MPI programmers
to use them whenenever possible, as high-quality implementations will
take advantage of this fact.
( End of advice to users.)
Advice
to implementors.
The range operations should be implemented, if possible, without
enumerating the group members,
in order to obtain better scalability (time and space).
( End of advice to implementors.)
| MPI_GROUP_FROM_SESSION_PSET(session, pset_name, newgroup) | |
| IN session | session (handle) |
| IN pset_name | name of process set to use to create the new group (string) |
| OUT newgroup | new group derived from supplied session and process set (handle) |
The function MPI_GROUP_FROM_SESSION_PSET creates a group newgroup using the provided session handle and process set. The process set name must be one returned from an invocation of MPI_SESSION_GET_NTH_PSET using the supplied session handle. If the pset_name does not exist, MPI_GROUP_NULL will be returned in the newgroup argument. As with other group constructors, MPI_GROUP_FROM_SESSION_PSET is a local function. See Section The Sessions Model for more information on sessions and process sets.